DAYA PADA RLC

Pengertian daya           : perkalian antara tegangan yang diberikan dengan hasil arus yang mengalir.      

Secara matematis         : P =VI Æ sumber searah atau DC

  Daya dikatakan positif, ketika arus yang mengalir bernilai positif artinya arus mengalir dari sumber tegangan menuju rangkaian (transfer energi dari sumber ke rangkaian )

  Daya dikatakan negatif, ketika arus yang mengalir bernilai negatif artinya arus mengalir dari rangkaian menuju sumber tegangan (transfer energi dari rangkaian ke sumber )

Daya Sesaat

Daya sesaat adalah daya yang terjadi pada saat hanya waktu tertentu ketika sebuah komponen mempunyai nilai tegangan dan arus yang mengalir padanya hanya saat waktu tersebut.

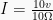
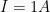
Daya Rata – Rata

Daya rata-rata adalah daya yang dihasilkan sebagai integral dari fungsi periodik waktu terhadap keseluruhan range waktu tertentu dibagi oleh periodanya sendiri.

Untuk melihat hasil daya rata-rata pada setiap komponen pasif yang dilaluinya menggunakan rumus yang telah kita pelajari pada bab sebelumnya tentang harga ratarata.

Daya Kompleks

Daya Rata – Rata (P)

Daya ini sebenarnya adalah daya yang dipakai oleh komponen pasif resistor yang merupakan daya yang terpakai atau terserap. Kalau kita perhatikan supply dari PLN ke rumah-rumah maka daya yang tercatat pada alat kWH meter adalah daya rata-rata atau sering disebut juga sebagai daya nyata yang akan dibayarkan oleh pelanggan.

Simbol :  P 

Satuan : Watt (W)

Secara matematis daya rata-rata atau daya nyata merupakan perkalian antara tegangan efektif, arus efektif, dan koefisien faktor dayanya. 

Daya Reaktif ( Q )

Daya ini adalah daya yang muncul diakibatkan oleh komponen pasif diluar resistor yang merupakan daya rugi-rugi atau daya yang tidak diinginkan. Daya ini seminimal mungkin dihindari kalaupun bisa diperkecil, walaupun tidak akan hilang sama sekali dengan cara memperkecil faktor dayanya. 

Simbol : Q

Satuan : Volt Ampere Reaktif (VAR)

Secara matematis daya reaktif merupakan perkalian antara tegangan efektif, arus efektif, dan nilai sin θ.

Daya Tampak ( S )

Daya yang sebenarnya disupply oleh PLN, merupakan resultan daya antara daya ratarata dan daya reaktif.

Simbol : S

Satuan : Volt Ampere (VA) 

Secara matematis daya tampak merupakan perkalian antara tegangan dan arus efektifnya

Daya kompleks

Merupakan gabungan antara daya rata-rata dan daya reaktifnya.

S = P + jQ 

RANGKAIAN LISTRIK KOMPLEKS

Carilah Nilai I ?

Jawab :

Bila kita melihat resistor R1, R2, dan R3 sebagai suatu rangkaian Δ (pada rumus berturut-turut Rab, Rac, dan Rbc) dan ingin menggantinya dengan rangkaian Y, kita bisa mengubah rangkaian jembatan ini menjadi rangkaian yang lebih sederhana yaitu rangkaian seri-paralel:

Sekarang kita telah mendapatkan rangkaian yang lebih sederhana. Kita bisa menganalisa rangkaian ini menggunakan aturan seri-paralel:

Serikan rangkaian RB dan R4 serta rangkaian Rc dan R5

RS1 = RB + R4

= 2Ω + 3Ω = 5 Ω

RS2 = RC + R5

        = 3Ω + 12Ω = 15 Ω

sehingga terbentuk rangkaian seperti ini:

Selanjutnya, hambatan RS1 dan RS2 di paralelkan

RS1// RS2 = RP =

Rp =  =  = 3 Ω

Dan terbentuk rangkaian seri seperti ini :

Dan rangkaian diatas dihitung secara seri menjadi RT

RT = RA  + RP

                       = 6 + 3 = 9 Ω

Lalu, hitung I dengan menggunakan hukum Ohm

HUKUM OHM

Contoh Soal 

Pada suatu rangkaian listrik sederhanan terdapat penyuplai daya dengan tegangan 10 volt dan beban dengan hambatan 10 ohm. Berapakah besarnya kuat arus pada rangkaian tersebut?

Pembahasan:

Dengan menggunakan hukum Ohm, kita dapat langsung mencari nilai kuat arus pada rangkaian sederhana dengan memakai rumus:

  

Jadi, kuat arus yang mengalir pada rangkaian tersebut sebesar 1 Ampere.

HUKUM KIRCHOFF 1

Contoh soal :

Pertanyaan: Berapakah I4?

Jawab:

Dari gambar rangkaian yang diberikan diatas, belum diketahui apakah arus I4 adalah arus masuk atau keluar. Oleh karena itu, kita perlu membuat asumsi awal, misalnya kita mengasumsikan arus pada I4 adalah arus keluar.

Jadi arus yang masuk adalah :

Arus yang keluar adalah :

I1 + I4 = 5 + I4

3 = 5 + I4

I4 = 3 – 5

I4 = -2

Karena nilai yang didapatkan adalah nilai negatif, ini berbeda dengan asumsi kita sebelumnya, berarti arus I4 yang sebenarnya adalah arus masuk.

HUKUM KIRCHOFF 2

Contoh Soal

a. Misalkan arah kuat arus kita anggap dulu berlawanan dengan arah loop

Σε + ΣI. R = 0
ε3 – ε2 + ε1 – I (R1 + R2 + R3) = 0
4 – 2 + 4 – I (15 + 5 + 10) = 0
6 – 30I = 0
30I = 6
I = 6/30 = 1/5 = 0,2 A

b. Tegangan antar a dan b (Vab)

Jika melalui jaluar adcb (panjang)
Vab = ε3 – ε2 – I (R3 + R2) (I negatif karena berlawanan dengan arah I total)
Vab = 4-2 – 0,2 (10 + 5)
Vab = 2 – 0,2 (15)
Vab = 2 – 3 = -1 V

Jika melalui jalur ab (pendek)
Vab = -ε1 + I R1 ( I positif karena searah dengan I total)
Vab = – 4 +  0,2 (15)
Vab = -4 + 3 = -1 V
Jadi tegangan antara titi  a dan b (Vab) = -1 V

ELEMEN AKTIF

Contoh Soal :

Tentukan keluaran dari gambar diatas, Bila diketahui R1= 24 Ω dan R2 = 2.4 K

Jawab :

                                           Vo = Vref {1 +(R2/R1)} + ladj.R2

                               

                                                   = 1.25 V {1+(2400/240)} + (100µA) (2400)

= 13.75 V + 0.24 V

= 13.99 V

RESISTOR

Contoh Soal :

Jika tiga buah resistor R1, R2 dan R3 dengan besar berturut-turut 50 ohm, 100 ohm dan 1 kohm. Hitunglah besar hambatan pengganti resistor tersebut jika ketiga resistor tersusun secara seri?

Pembahasan :

Diketahui :

R1 = 50 ohm

R2 = 100 ohm

R3 = 1 kohm = 1000 ohm

Ditanya : Resistor Pengganti atau Resistor total dari ketiga resistor yang tersusun secara seri?

Gunakan Rumus Resistor Seri

Rs = R1 + R2 + R3 + ... + Rn

Karena ada 3 resistor yang tersusun secara seri (n = 3) maka

Rs = R1 + R2 + R3 =50 ohm + 100 ohm + 1000 ohm =1150 ohm = 1,15 kohm

Jadi besarnya resistor pengganti yang tersusun secara seri adalah 1150 ohm atau 1,15 kohm.

INDUKTOR

Contoh Soal :

 Dalam sebuah induktor yang memiliki panjang 20 cm, jumlah lilitan 500 lilitan, dan luas penampang 2 . Besar induktansi diri kumparan tersebut adalah ?

Untuk menjawab soal ini, bisa kita gunakan rumus besar induktansi kumparan jika dialiri arus yang berubah-ubah.

Besaran panjang kumparan dan luas kumparan satuannya harus dirubah terlebih dahulu ke dalam satuan internasional

Besar induktansi diri pada kumparan adalah

KONDUKTOR

Contoh Soal :

Potensial disuatu titik yang berjarak r dari muatan Q adalah 600 V. Itensitas medan listrik di titik tersebut 400 N/C. Tentukan besar Q?

Jawab :

Potensi Listrik V(r) = 600 V dan Medan Listrik E(r) = 400 N/C. Maka

            V = Er a r = V/E = 600/400 = 1.5 m. maka 

            V(r) = Kq/r

            600 = 9 x 10⁹ x q/1.5 

            q = 10⁻⁷ C